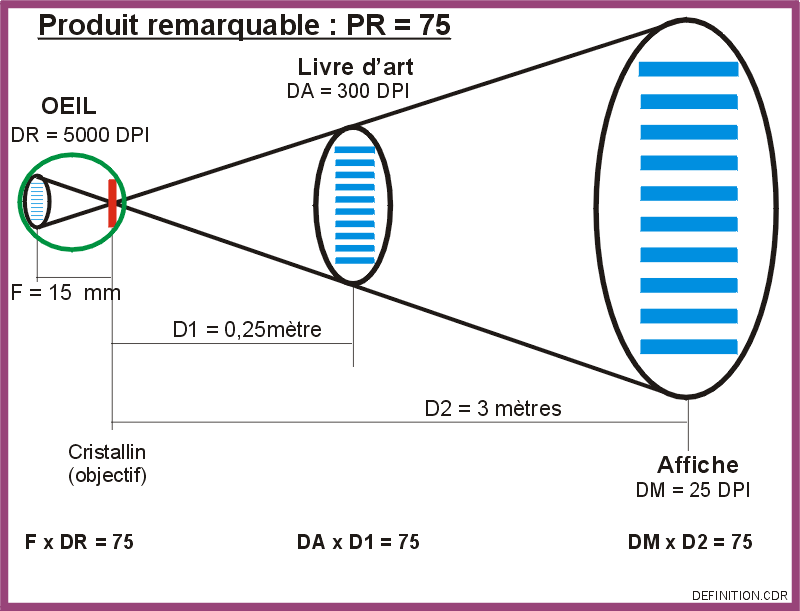
Représentation du produit remarquable définition x focale
de l'oeil avec deux applications classiques.
| Retour menu |
L'IMAGE ET SA STRUCTURE.
QUELQUES GRANDEURS PHOTOGRAPHIQUES ET LEURS RAPPORTS.
Les questions relatives à la vision, au graphisme, à la taille, à la résolution des images et à la définition des écrans sont fréquentes. Voici quelques éléments de définitions et de relations entre grandeurs, rédigés comme aide-mémoire, à notre usage personnel, pour comprendre.
Navigation directe vers les rubriques
| Physiologie oculaire | Définition rétinienne | Applications |
| Profondeur de champ | ||
| Technique écrans | ||
| Focale équivalente |
L'œil, c'est une chambre photographique dont les caractéristiques communément admises sont le suivantes :
Sources
: http://www.snof.org/vue/av.html
http://docinsa.insa-lyon.fr/these/2004/chain/10_annexes.pdf
http://www.sciences.univ-nantes.fr/physique/enseignement/DeugA/Physique1/optique/cours/chap6.htmlhttp://acces.inrp.fr/acces/ressources/neurosciences/vision/de_visu/soutien_scientifique_devisu/retine-centrale-et-retine-peripherique
Distance focale
de l'objectif (le cristallin plus la cornée, 60 dioptries) : F = 15 mm environ.
Diamètre moyen d'un "pixel" physiologique, cône ou bâtonnet
: 5 microns environ.
- La rétine
tapisse environ 75% de la surface interne de l'œil et cela aboutit à
une surface de plusieurs centimètres carrés. Mais les spécialistes
distinguent deux types de rétine, on pourrait presque dire trois :
- La rétine périphérique.
Composée exclusivement de bâtonnets. C'est la plus grande partie,
celle qui nous sert à voir par faible luminosité et surtout à
détecter les mouvements jusqu'au bord de notre champ visuel. Elle comprend
effectivement environ 120 millions de bâtonnets, qui ne donnent pas d'image
nette mais augmentent la sensibilité au détriment de la résolution
spatiale. Elle sert "à
voir".
- La rétine centrale. C'est le domaine de la
vision en pleine lumière. Elle a une bonne résolution spatiale,
au détriment de la sensibilité. Elle comprend environ 6 millions
et demi de cônes et bâtonnets, mais les cônes sont largement
dominants... Sa forme est une ellipse horizontale de 1,5 mm de largeur sur 1
mm de hauteur.
C'est elle qui détermine le champ de 1° environ, appelé "champ
de vision nette". Elle sert "à regarder".
- La fovea. C'est le centre de la vision
d'analyse, le plus précis. Elle fait environ 200 µ de diamètre.
Composée exclusivement de cônes groupés en mosaïque
hexagonale régulière, c'est sur elle que le système de
commande des yeux va orienter et focaliser l'image de l'objet. Mais son champ
est faible : environ 3 minutes d'arc... C'est elle qui permet de définir
le pouvoir séparateur de l'œil standard communément
admis comme étant égal à 1 minute d'arc. Elle sert "à
analyser".
Définition
rétinienne :
La surface sensible est la macula lutea, ou tache jaune, zone de la
rétine contenant la zone de plus haute définition :
la fovea centralis, dont la définition rétinienne DR
est, pour des cônes
de 5 µ de diamètre (0,005mm) à la base :
DR = 1
mm / 0,005 = 200 points par millimètre = 5000 DPI.
Profondeur de champ et netteté
Les différents ouvrages techniques et FAQ's d'Internet définissent la profondeur de champ comme l'espace d'image nette entre des plans situés à des distances différentes, déterminées à partir de la défocalisation d'un point image qui s'agrandit progressivement en cercle dès que l'on s'écarte du plan focal. Le cercle ainsi défini (c) est appelé "cercle de confusion". Il est déterminé expérimentalement et les valeurs retenues par deux grandes marques servaient de référence.
Pour Zeiss et Sinar, des valeurs anciennes, valables pour les chambres grand format du début du 20e siècle, donnent c = 1/1730 de la diagonale du format.
Cette
valeur fut reprise par la généralité des constructeurs
pour les tables de profondeur de champ... Quelle
est sa correspondance en matière de définition angulaire (Da)
? Da
= arctg 1 / 1730 = 2 minutes d'arc environ.
Est-ce que cette valeur est convenable pour qu'un image offre une sensation
de réalisme, de "piqué", de sécheresse,
en tout cas de netteté parfaite ?
Notre réponse est négative, et voici pourquoi :
Le
cercle de confusion conventionnel sous-entend une définition angulaire
de 2 minutes d'arc, alors que la définition angulaire de l'oeil est universellement
reconnue comme étant de l'ordre de la minute d'arc.
Le rapport de 2 entre ces valeurs est totalement illogique et probablement dicté
par des considérations purement commerciales.
Angle de champ
René Bouillot (1) exprime à juste titre l'angle de champ seulement
dans le plan horizontal.
Prenons l'exemple d'un capteur
numérique, associé avec deux objectif, l'un de 50 mm, l'autre
de 28 mm de focale :
Capteur : H = 23,7 x V = 15,2
Objectifs de focales F = 50 et 28 mm
La formule donnant l'angle de champ est de la forme : Alpha (horizontal = 2 * Arc Tg ( H / 2F )
Soit pour le 50 mm : 2 x ATN ( 23,7 / (2 x 50 ) = 26° 40'
et pour le 28 mm : 2 x ATN ( 23,7 / (2 x 28 ) = 45° 52'
(1) "La pratique du reflex numérique"
René Bouillot
Eyrolles/VM 2006 ISBN : 2-212-67269-1
|
Si la transition entre deux zones de densités ou de couleurs différentes occupe sur la rétine une dimension égale ou inférieure à celle d'un cône de la fovea centralis, la sensation de netteté sera parfaite. Si, au contraire, cette transition s'étale sur plusieurs cônes voisins, la netteté paraîtra moins piquée, plus molle, plus floue. Pratiquement, si une image parait nette et piquée, cela signifie aussi que l'on peut s'en rapprocher en découvrant plus de détails. A la condition évidente de ne pas se rapprocher plus près que la distance minimum d'observation impliquée par la résolution propre du document... Ni plus près que la distance imposée par son punctum proximum personnel ! |
Notons au passage que les imprimeurs, grands techniciens pratiques, demandent des documents en 300 DPI minimum pour les impressions des ouvrages de qualité. Ce qui correspond à un impact rétinien du pixel de (25,4 / 300) / 250 x 15 = 5 microns. Soit très exactement le diamètre d'un cone... Vous pensez réellement qu'il puisse s'agir d'un hasard ?
C'est
dû à l'augmentation du diamètre de la tache de diffraction,
ou tache d'Airy, qui représente le diamètre de l'image obtenue
d'un point lumineux théorique parfait, en fonction des lois physiques
et du diamètre du diaphragme.
En simplifiant
et en arrondissant, on peut écrire D = 0,7 n où D = diamètre
de la tache et n = chiffre du diaphragme.
Ceci, pour une valeur centrale du spectre des couleurs visibles.
Ainsi, un bon objectif, diaphragmé à f:22 donnera une tache de diffraction de D = 0,7 x 22 = 15 microns environ.
A partir de ces éléments, nous pouvons déterminer le diamètre des cercles de confusion réalistes pour deux formats de capteurs. Pour la distance focale normale, on prendra la valeur de la diagonale du format considéré. Rappelons que pour qu'une image paraisse parfaitement nette, il suffit que le diamètre du cercle de confusion ne dépasse pas 5 microns (taille du photosite de l'oeil : le cône) multipliés par le rapport focale / focale oeil.
1°
Observation d'un document tenu à la main, à une distance de 25
cm.
Diamètre
max du point : 5 x 250 / 15= 83 microns. DPI : 25,4 / 0,083 = 306 DPI (Juste
la valeur des imprimeurs !).
2°
Film 24 x 36 mm, diagonale du format = 43 mm.
Diamètre max du cercle de confusion, C
= 5 x 43 / 15 = 15 microns (et non pas 30 !)
3°
Capteur numérique (Canon 20 D) de 22,5 x 15 mm, Largeur capteur = 22,5
mm pour 3504 pixels.
Diamètre max du photosite (donc du cercle
de confusion admissible), C = 22,5 / 3504 = 6,4 microns
Nous remarquons immédiatement que nos exigences en matière de cercle de confusion maximum admissible sont deux fois plus sévères que la valeurs communément admise en 24 x 36 mm. Lors de la prise de vue sur appareil conventionnel dont l'objectif porte une graduation de profondeur de champ, nous considérons que cette échelle est fausse et que la profondeur de champ sera en réalité la moitié de celle indiquée. Alors, considérations commerciales ?
A
partir de ces deux chiffres, la définition rétinienne et la focale
de l'oeil, nous pouvons définir un produit remarquable PR.
PR = Focale œil x Définition rétinienne = 15 x 200 = 3000.
Ce chiffre : 3000, est valable pour ces mesures physiques.
Pour les informaticiens, plus accoutumés aux DPI, si nous exprimons la
définition rétinienne en DPI et les distances en mètres,
nous obtenons : PR = 5000 x 0,015 = 75.
C'est ce chiffre PR = 75 que nous utiliserons, en précisant son rôle
à l'aide d'exemples.
Le produit remarquable permet de calculer la définition nécessaire et suffisante d'un objet pour qu'il apparaisse parfaitement NET à l'observation usuelle (puisque toute augmentation de la définition ne pourrait être utilisée, car produisant sur la macula des détails inférieurs à la dimension des cônes).
Définition
nécessaire Dn, en fonction de la distance d'observation Do.
Dn = 75 / Do (m).
Définition nécessaire, en DPI = 75 / Distance d'Observation, en mètres

Représentation du produit remarquable définition
x focale
de l'oeil avec deux applications classiques.
NOTA : Cette méthode convient pour l'observation d'images particulièrement nettes. Sur une mire à traits parallèles, le contraste entre traits noirs et fond blanc sera proche de 100% et la mire paraîtra "piquée". ll n'en serait pas de même si l'on cherchait à pousser la résolution du système près de son maximum : le contraste deviendrait très faible : de l'ordre de 10 %. C'est la méthode de l'Institut d'Optique qui, dans le mode d'emploi des mires de Foucault, recommande de s'éloigner jusqu'à ce que l'on puisse tout juste indiquer l'orientation de groupes de traits. Cette limite est facilement mesurable. Les distances obtenues sont en gros le double de celles de notre formule.
Sur les courbes de transfert, nous retenons le chiffre de la fréquence maximale pour un contraste de 50 %. C'est une simplification strictement personnelle permettant des comparaison faciles et immédiates d'objectifs.
-
Prenons un video-projecteur, réglé pour obtenir
une image de mire (Institut d'Optique, par exemple) parfaitement nette sur un
écran placé à une distance de 1 mètre. Notre point d'observation est situé à la
verticale du video-projecteur. Dans ces conditions, l'analyse de la mire permet de fixer la limite
de visibilité des séries de traits au
carré n° 8, par exemple.
-
Si on recule l'écran, à 2 m, puis à 4 mètres on
constate que la limite se situe toujours vers le carré N° 8.
Alors même que
la dimension des traits sur l'écran est multipliée par 2 puis par 4.
(C'est la surface sur l'écran qui se trouve
multipliée par 4 puis par 16).
Bien sûr, mais comme la distance a été augmentée
dans le même rapport, la largeur angulaire d'un trait reste inchangée et se projette avec une dimension
constante sur la fovea centralis.
Vous
visitez une exposition photographique, constituée de posters de 75 x
100 cm. Pour l'observation optimum, vous vous êtes placé à
1,5 m de l'image. Définition nécessaire de cette image : Dn =
75 / 1,5 = 50 DPI
Autre cas, vous tenez à la main un 30 x 40 cm que vous observez à
25 cm : DN = 75 / 0,25 m = 300 DPI
Nota important : vous remarquerez dans ce dernier exemple que nous obtenons la valeur demandée par les imprimeurs pour l'impression de photographies dans des ouvrages tenus à la main, soit 300 DPI. La distance d'observation de 0,25 m, qui paraitra un peu courte à beaucoup, est la distance d'observation minimale moyenne dans l'espèce humaine. C'est la distance appelée "punctum proximum".
Autre
exemple. Hypnotisés par l'écran bleu du crash Windows, vous êtes
environ à 0,70 m de votre 17 pouces favori... Des fumerolles sortent
de vos oreilles...Non, elle n'interviennent pas dans la formule, sauf comme
facteur de décompression des surpressions internes...
Ecran d’ordinateur, observé à 0,73 mètre. Pitch de l’écran = 0,25 mm
La
définition intrinsèque d’un écran est égale à la division de la
longueur d’un inch (en mm = 25.4) par la valeur du pitch, en mm (Le
pitch est la distance séparant deux triades colorées sur la dalle de
l’écran d’un ordinateur). Le pitch est indiqué dans les spécifications
techniques ou même peut se mesurer très facilement.
Définition physique de l’écran : D = Inch / Pitch = 25,4 / 0,25 = 102 DPI
Définition nécessaire de cette image : Dn = 75 / 0,73 = 102 DPI Un hasard ? Mmmh
Sur cet écran, une image de 1280 x 1024 pixels aura une dimension de :
Largeur 1280 x 0,25 = 320 mm et une hauteur de H = 1024 x 0,25 = 256 mm.
Si l’écran est plus petit que cela, elle débordera des limites et s’il
est plus grand, elle n’en occupera qu’une partie. Rappellons que la
définition intrinsèque, physique de votre tube cathodique ou de votre
écran LCD est de :
Unité
(mm) / pitch (mm). Exemple : les spécifications techniques de votre 17
pouces favori annoncent un pitch de 0,20 mm.
La définition maximale que sera capable d'afficher ce tube sera de 25,4/0,20
= 127 DPI Nous butons là sur la définition intrinsèque
du tube cathodique ou de l'écran à cristaux liquides. Vous pouvez
toujours lui appliquer des images de plus hautes définitions, l'image
observée sera toujours physiquement limitée par la définition
propre de votre écran.
Nota : Le
chiffre de 72 DPI qui est souvent pris en compte pour la définition des
écrans n'est plus d'actualité ! C'est une survivance due aux premiers tubes qui affichaient
gaillardement de pitches de 0,35 mm... Les tubes actuels (2009) ont des pitches
de 0,20 à 0,24 mm, soit des définitions de 104 à 127 DPI.
Ces valeurs se retrouvent sur les écrans plats.
![]() Pour
vérifier la structure de nos tubes couleurs, il suffit de prendre une
loupe : le point couleur n'existe pas : on mesure environ 4 groupes de 3 points
en couleurs élémentaires rouge, vert et bleu par millimètres.
L'oeil est incapable de distinguer séparément les composant de
chaque groupe. Il les fusionne en fonction de leur intensités relatives
dans le groupe, constituant pour l'observateur un seul point lumineux coloré.
Ce qui permet de dire que le pitch de cet écran est d'environ 1 / 4 =
0,25 mm. A quelle définition physique cela correspond-t-il ? La définition
s'exprimant en DPI, il suffit de diviser la longueur d'un pouce, soit 25,4 mm
par la valeur du pitch : DPI = 25,4 / 0,25 = 100 DPI environ.
Pour
vérifier la structure de nos tubes couleurs, il suffit de prendre une
loupe : le point couleur n'existe pas : on mesure environ 4 groupes de 3 points
en couleurs élémentaires rouge, vert et bleu par millimètres.
L'oeil est incapable de distinguer séparément les composant de
chaque groupe. Il les fusionne en fonction de leur intensités relatives
dans le groupe, constituant pour l'observateur un seul point lumineux coloré.
Ce qui permet de dire que le pitch de cet écran est d'environ 1 / 4 =
0,25 mm. A quelle définition physique cela correspond-t-il ? La définition
s'exprimant en DPI, il suffit de diviser la longueur d'un pouce, soit 25,4 mm
par la valeur du pitch : DPI = 25,4 / 0,25 = 100 DPI environ.
Mais quel que soit le nombre de pixels d'une
image appliquée à l'écran par l'électronique, la
définition observée de cette image ne dépassera
jamais la définition physique de cet écran. Donc pour afficher
seulement à l'écran, il est pratiquement inutile de dépasser
100 DPI. En effet, la présence du masque fera que vous ne verrez pas
tous les points illuminés par le faisceau d'électrons, mais seulement
ceux pour lesquels le faisceau passe devant un trou !
Et pourtant l'image observée sur
l'écran apparait comme parfaitement nette . La raison est simple
: quel est l'écart entre deux point lumineux (ou triade colorée
R, V, B.) ? Usuellement, en 2009 : 0,25 mm. Ce qui donne 25,4 / 0,25 = 100 points
/ inch qui, observés à 75 cm, donnent un produit remarquable de
100 x 0,75 = 75.
Le même produit remarquable que celui de l'oeil ! Coïncidence ? Sûrement pas. Les constructeurs savent bien qu'il serait inutile d'augmenter la définition des tubes cathodiques ou des écrans à cristaux liquides, puisque, à cette distance moyenne d'observation, l'oeil serait dans l'incapacité de percevoir cette augmentation !
En corollaire, toute définition d'image inférieure à celle du masque se traduira par une diminution de la netteté, jusqu'à ce qu'on atteigne la visibilité de la pixellisation et le grandissement progressif des pixels de l'image électronique.
Résolution des écrans
LCD
![]() D'après
la notice technique d' un Proview 17 pouces, la résolution de sa dalle
est de 1280 x 1024 points lumineux colorés ou "pixel" (un pixel
= une triades R-V-B). Le pitch est donné (aussi bien en V qu'en H) comme
P = 0,264 mm. En mesurant la partie utile
de la dalle, on trouve 338 mm en horizontal. Et 338 mm / 0,264 = 1280 points
lumineux.
D'après
la notice technique d' un Proview 17 pouces, la résolution de sa dalle
est de 1280 x 1024 points lumineux colorés ou "pixel" (un pixel
= une triades R-V-B). Le pitch est donné (aussi bien en V qu'en H) comme
P = 0,264 mm. En mesurant la partie utile
de la dalle, on trouve 338 mm en horizontal. Et 338 mm / 0,264 = 1280 points
lumineux.
La résolution "native", originelle, de cette dalle est de 1280
x 1024. Sur un écran cathodique,
chaque point lumineux est excité lors du passage du pinceau d'électrons
focalisés au travers des trous du masque. Puis il s' ETEINT et attend
le prochain balayage. Ce qui explique le scintillement parasite avec des fréquences
de balayage trop basses.
Sur un écran LCD, il en va tout autrement ! Le pixel est maintenu ÉCLAIRÉ par un transistor après son activation par l'adressage. Et luminance et couleur restent constantes jusqu'à ce qu'un nouvel adressage change éventuellement leurs valeurs...
Démonstration pratique : la photographie d'écran
de moniteur.
Avec un appareil numérique, on photographie un écran LCD à
différentes vitesses (en laissant le diaphragme en automatique). Par
exemple, de 1/20e de seconde à 1/200e de seconde (à 800 ISO).
Toutes les images seront impeccablement exposées.
La même opération sur un écran à
tube cathodique donnerait des résultats catastrophiques à partir
de 1/30e de seconde.
Taille des fichiers et de l'image à l'écran et en impression.
C'est une question récurente sur les forums et dans le courrier : "comment régler les DPI pour avoir une image d'une certaine taille, sur l'écran ou imprimée ? ". Mis à part le fait que ces pauvres DPI sont mis à toutes les sauces, même dans celles où ils n'ont vraiment rien à faire, cela traduit un souci et une incompréhension technique des phénomènes mis en cause. Essayons de clarifier ces notions par des exemples appliqués et détaillés :
Taille des fichiers
Soit une image dont le nombre de pixels est de 2010 x 1410 = 2 834 000 pixels. Si on a scanné en haute résolution couleur (16 000 000 de couleurs = codage en 24 bits), voire plus, le fichier obtenu fera 2 384 000 x 24 = 68 000 000 de bits. Comme les dimensions des fichiers sont exprimées en octets (8 bits), la taille du fichier obtenu est de :
Taille du fichier graphique : 68 000 000 / 8 = 8,5 Millions d'octets.
NOTA Nous avons détaillé ce calcul car c'est un point ou il y a beaucoup de confusions.
Pour clarifier encore, supposons que la taille du fichier soit considérée comme trop importante et que l'on souhaite la réduire sans toucher à la définition de l'image. Il suffira de réduire le nombre de couleurs de l'image.
Si on la réduit (traitement graphique) en 256 couleurs, soit en 8 bits, la taille du fichier deviendra : 8,5 Mo / (24 bits/8 bits) = 2,8 Mo. On pourrait aller beaucoup plus loin en adoptant un format graphique comprimé, genre JPEG, avec perte d'information, mais cela ne conviendrait plus aussi bien pour une impression, bien que cela paraisse très correct à l'écran (d'une définition toujours assez faible : 70 à 100 DPI).
Taille
affichage Soit un écran de 19 pouces,
dont le balayage, bien réglé pour aller jusqu'aux bords, est de
1280 x 960 pixels ou points élémentaires. Une ligne horizontale
du balayage comprendra donc 1280 points. On souhaite y appliquer une image de
700 x 525 pixels et connaître les dimensions qu'elle aura, sur l'écran.
Le tube de 19 pouces fait environ 366 mm
en horizontal. Son pitch (espace entre deux triades colorées successives)
est de 0,26 mm, ce qui donne en largeur un nombre physique de points lumineux
de 366 / 0,26 = 1400 points environ. Sa définition visuelle maximale
sera environ 1400 points / 14,4 inches = 97 DPI.
Et cela quelles que soient les caractéristiques
des fichiers graphiques appliqués.
Dans ces conditions, l' image de 700 pixels occupera 700 / 1280 = 54% de la
largeur de l'écran, soit 366 x 0,54 = 198 mm
de large environ (sous réserve que l'échelle de zoom écran
soit bien de 100 %, sinon tenir compte du coefficient).
Si on décide de passer le balayage
en 800 x 600, toutes autres choses inchangées : l'image sur l'écran
devient
700 / 800 = 0,875. Ce qui donne une largeur de 366 mm x 0,875 = 320 mm. L'image
sera plus grande.
Les conclusions sont immédiates, les dimensions à l'écran dépendent :
1° du mode
de balayage
2°
de la dimension de l'écran
3° des dimensions de l'image, en pixels
4° du grossissement (zoom) choisi pour le logiciel graphique.
Formule :
Largeur
à l'écran = Largeur de l'écran (mm) x largeur fichier
(pixels) x coeff. zoom / largeur du balayage (pixels) |
Application :
Pour un fichier de 3200 x 2400 pixels, zoom de 25 %, sur un écran de 338 mm de largeur, balayé en 1024 x 768 :
Largeur
image à l'écran = 338 mm x (3200 pixels x 0,25) / 1024 pixels
= 264 mm |
Taille impression Pour imprimer ce même fichier graphique de 700 x 525 pixels (que nous supposons issu d'un scanner sous 300 DPI), si nous choisissons un coefficient d'échelle de 100 % pour l'imprimante, l'impression aura les dimensions suivantes :
Largeur
: 700 pixels / 300 DPI = 2,33 pouces. Soit en millimètres : 2,33 x 25,4
= 59,3 mm
Hauteru : 525 pixels / 300 DPI = 1,75 pouce. Soit en millimètres : 1,75
x 25,4 = 44,5 mm
Si
nous avions estimé l'impression trop petite pour nos besoins, il aurait
suffit de choisir un
coefficient d'échelle de 400 % et les nouvelles dimensions auraient été
les suivantes : 237,2 x 178 mm.
(Attention toutefois à ne pas trop pousser : image moins nette et risques
d'apparition de la pixellisation)
Les dimensions
d'impression sont fonction de :
1° des dimensions de l'image, en pixels
2° de la définition d'impression
3° du coefficient
d'échelle du programme graphique.
Formule :
Largeur
imprimée = Largeur fichier (pixels) / Définition impression
(DPI) x coefficient d'échelle x 25,4 (mm) Hauteur imprimée = Hauteur fichier (pixels) / Définition impression (DPI) x coefficient d'échelle x 25,4 (mm) |
Si on numérise au maximum des possibilités des scanners (on arrive souvent à des fichiers de 30 Mo et plus), cela permet de laisser le maximum de possibilités au traitement graphique qui suit. Cependant, la règle générale donne la formule suivante :
Résolution de numérisation = Résolution du périphérique de sortie x Facteur d'échelle.
Exemple : pour imprimer en A4 en 300 DPI, à partir d'un 24 x 36 mm :
Facteur d'échelle est de 297mm / 36 mm = 8,25.
D'où la définition de numérisation : 300 x 8,25 = 2500 DPI (environ).
Cette règle peut se modifier en fonction de certains impératifs d'impression professionnels qui font appel au tramage. On évite alors d'avoir une résolution de numérisation égale à la fréquence de trame. On tient compte d'un "Facteur de qualité" = coefficient résolution / trame. Ce facteur vaut usuellement de 1,5 à 2.
Résolution de numérisation = Résolution de sortie X facteur de qualité x facteur d'échelle
Les scanners paraissent poser des problèmes quand au choix des réglages, en particulier pour scanner des diapositives. Quelle définition choisir ? Numérisez au maximum de définition, et ensuite adaptez votre image à vos besoins avec un logiciel de traitement graphique. Mais beaucoup d'utilisateurs voudraient avoir directement l'image prête à être utilisée, sans manipulations supplémentaires.
Raisonnons à l'envers, à partir du document final attendu. Supposons que l'on veuille publier une illustration dans une revue format A4, imprimant à 300 DPI et que l'on souhaite que la photo occupe une demie page, soit environ 170 mm x 120 mm.
Dimensions photo, en pouces (inches) : 170 /25,4 = 6,7 et 120 / 25,4 = 4,7
Dimensions du grand coté en pixels : 6,7 x 300 DPI = 2010 pixels
Dimensions du petit coté en pixels : 4,7 x 300 DPI = 1410 pixels
Coefficient d'échelle du scanner : le cliché d'origine 24 x 36, fait donc 36 mm de largeur. Rapport d'agrandissement (largeur finale /largeur départ), ou échelle = 170 / 36 = 4,7 , d'ou, en prenant un facteur de qualité FQ de 1,5 pour l'impression :
| Définition scanner = définition finale x échelle x FQ = 300 DPI x 4,7 x 1,5 = 2100 DPI environ. |
Les scanners pour diapositives ayant une définition réglable dont la valeur maximale dépasse 2700 DPI, il est possible de réaliser cette numérisation.
Le film 35 mm, négatif ou positif, noir et blanc où couleur, conditionné en bandes ou en montures diapositives, est dans tous les cas un support transparent.
Les scanners à plat, très répandus, sont des scanners à réflexion alors qu'il faut pour scanner un film, utiliser des scanners à transmission. De plus, la faible taille de la surface active (environ 9 centimètres carrés) implique une haute définition afin de pouvoir produire des images de grandes dimensions. Ceci exclue les "Dos pour transparents" parfois vendus en compléments des machines de début de gamme (ce dispositif est destiné à scanner des ektachromes de grande taille).
A partir de la matière brute, issue de la numérisation, il y a toujours des améliorations à apporter à l'image : taille, luminosité, contrastes, correction de dominantes, nettoyage, recadrage, renforcement (de la netteté) etc... C'est l'objet du traitement graphique. Signalons un défaut courant survenant lors du renforcement d'une image à faible définition : l'aliasing, ou crénelage, ou encore aspect "en escalier" des diagonales.
Voici un processus très simple permettant
de matérialiser son apparition :
Une même photo scannée deux fois, donne les fichiers suivants,
en fonction de la définition retenue :
A 100 DPI : fichier-1.TIF 594 x 390 pixels 227 Ko 15,09 x 9,81 cm
A 600 DPI : fichier-2.TIF 3568 x 2346 pixels 8 Mo 15,10 x 9,93 cm
Le fichier 600 DPI est ramené à 100 DPI et 594 x 390 pixels, pour
avoir à l'écran les mêmes dimensions que l'autre image. La
comparaison simultanée de ces deux photos, donne des résultats
absolument identiques à l'écran. Ce qui est conforme
à la théorie puisque l'écran utilisé a une définition
physique de 97 DPI.
Par contre, si l'on essaie de renforcer l'image à faible définition ce sont les accentuations qui provoquent le crénelage des diagonales sur l'image. Cette constatation a beaucoup moins d'effets sur l'image à 600 DPI, dont les résultats sont excellents, même après accentuation. Par contre, si on applique cette accentuation après réduction à 100 DPI, on retrouve le même défaut. Donc, toujours effectuer les corrections d'image en haute résolution.
Une image est faite dans l'instant et il faut la pérenniser, et cela dans les meilleures conditions possibles. Tout le monde connaît ces vieilles photos jaunies (que nos moyens modernes savent merveilleusement régénérer...) Il faut donc un moyen de conservation et le CD-ROM numérique est actuellement le meilleur. Mais quelles utilisations peut-on prévoir pour dans vingt ou vingt-cinq ans, par exemple ?
Visualisation à l'écran ? Même en anticipant sur une évolution technique prévisible, une définition d'une centaine de DPI devrait toujours suffire. Si, par contre, on souhaite une possible impression en haute résolution, 300 DPI suffisent et comme cette valeur est liée aux paramètres physiologiques de l'oeil, on est en droit d'espérer une certaine stabilité... Coté dynamique des gris ou de la couleur, avons-nous réellement besoin de stocker en 16 millions de couleurs ? Dans bien des cas, 65000 suffiront, voire 256 !
Pour la visualisation écran, le format JPG est le plus pratique, Vous devez pouvoir obtenir des images excellentes en 640 x480, qui occuperont moins de 50 Ko. Il faut se souvenir que JPG dégrade l'image et qu'il ne sera plus possible de retrouver la qualité originale, en haute résolution. Pour une impression future, confronté à ce problème, nous avons retenu le format TIF et les images font une dizaine de Mo. C'est un peu lourd, mais c'est le prix à payer pour la sécurité.
Actuellement (2020), SSD amovibles, cartes SD et clés USB sont imbattables.
La projection vidéo pose souvent des problèmes concernant la taille de l'image projetée ainsi que celle de sa luminosité.
La taille de l'image projetée dépend du projecteur et de la focale de l'objectif utilisé. Il est fréquent de rencontrer une salle possédant déjà son écran. Ce sont ses dimensions qui vont déterminer la position du projecteur dans les cas d'une focale fixe. Un zoom permettra une certaine souplesse en ce domaine, mais perdra tout avantage en matière de luminosité de l'image. En effet, l'ouverture des zooms est toujours plus faible que celle d'un objectif à focale fixe. Si un objectif présente souvent une ouverture de 2,0 à 2,8, celle des zooms est plus proche de 4.0 à 5,6, soit un écart moyen de 2 diaphragmes, soit encore (à source lumineuse identique) 4 fois moins de lumière sur l'écran de projection...
L'énergie lumineuse en sortie du projecteur est indiquée en Lumens. L'éclairement de l'écran est donné par la formule : Lux = Lumens / S. (S étant la surface éclairée de l'écran).
La brillance ou luminance de l'écran dépend de son coefficient de réflexion R (souvent de l'ordre de 0,8). Elle est donnée par la formule : Luminance (en candela par m²) = Eclairement x R
Ce terme revient souvent dans la littérature photographique numérique, mais paraît poser certains problèmes d'interprétation. Prenons, pour simplifier, un exemple appliqué :
Soit deux appareils, F100 et D1, équipés du
même objectif, un 50 mm, f=1,4.
Les "surfaces sensibles", film et capteurs ont des surfaces différentes
:
Pour le film 35 mm : 24x 36 mm = 8,6 cm carrés environ.
Pour le capteur = 3,7 cm² (d'après le C.I.). Le rapport de ces surfaces
est d'environ 2,3.
Les objectifs étant identiques et leurs diaphragmes réglés sur les mêmes ouvertures, 5,6 par exemple, s'ils photographient la même scène, un grand mur homogène, couvrant tout le champ 24 x36, l'éclairement en LUX, reçu par les surfaces sensibles SERA LE MEME dans les deux cas.
Simplement on en utilisera une plus ou moins grande surface, mais l'éclairement unitaire du film ou du capteur, par mm², restera IDENTIQUE. L'exposition n'a pas de raisons d'être différente. Commentons un peu :
1° Le capteur ayant une surface plus petite que celle du
film, n'enregistrera qu'une partie de l'image totale. Dans notre exemple, avec
50 mm de focale et une diagonale de film de 43 mm, cela induit un angle de prise
de vue de 46°30' environ.
2° Dans le cas du capteur, nous obtenons : diagonale = 28,4 mm environ.
Angle de prise de vue : 31° 42'.
Donc, nous n'aurons pas le même champ couvert et les deux images ne
seront pas identiques.
Calcul de la focale équivalente.
A quelle focale correspondrait, en 24 x 36 cet angle de 31° ?
Faisons le calcul inverse et l'on obtient F = 76 mm environ.
C'est la FOCALE EQUIVALENTE en 24 x 36 mm. C'est à dire qu'une photographie prise avec le F 100, dans les même conditions, depuis le même point, en 24 x 36 mm, avec une focale de 76 mm, montrera la même image que celle prise avec le D1 et sa focale de 50 mm.
Les conditions d'exposition seront-elles identiques ?
OUI, pour le D1, avec sa focale de 50 mm, équivalente à un 76
mm.
OUI, pour le F 100 dont nous avons changé la focale physique, réelle,
pour la porter à 76 mm. (Le diaphragme étant le même, le
rapport F/D n'a changé, D ayant aussi augmenté).
Ceci explique la différence entre
les objectifs des appareils argentiques et numériques : du fait de la
faible dimension des capteurs par rapport à la surface d'un 24 x 36 mm
, il y a réduction obligée de la focale afin de couvrir le même
champ.
|
La
focale ne change pas avec le senseur retenu pour photographier, film
24 x 36 mm ou capteur d'APN. |
La bonne exposition, ou lumination, d'un capteur ou d'un film (pour les appareils et dos argentiques) dépend :
de l'éclairement du capteur, en Lux, pendant l'ouverture de l'obturateur.
de la durée de cet éclairement (temps de pose T, en secondes).
de la sensibilité intrinsèque ISO du capteur (ou du film).
de la sensibilité affichée (qui peut différer de la sensibilité intrinsèque).
de la nature du post-traitement appliqué au signal capteur ou au traitement qui sera appliqué au film.
La lumination du film ou du capteur est fonction de la combinaison de ces données. Elle s'exprime en Lux x secondes et rentre dans le calcul de l' indice de lumination IL (ou EV = exposure value). La formule complète est de la forme :
IL = (log Lux + log ISO - k) / log 2.
k, coefficient standard d'atténuation et d'adaptation de formules = 2,44
Quelle est la lumination requise par un capteur ou un film noir et blanc 100 ISO ?
La norme NF S 22023 définit pour un sujet gris moyen, de 18 % de coefficient de réflexion, une valeur de lumination H, fonction de la sensibilité film en ASA, égale à :
H = 8 / ASA, d'où H = 8 / 100 = 0,08 Lux.Seconde
Soit encore un éclairement de 8 Lux, pendant une durée de 1/100e de seconde.
Des grandeurs photographiques...
En photographie, certaines grandeurs sont bien connues : un plein soleil moyen provoque sur Terre un éclairement de 50000 Lux et peut, dans certaines circonstances (neige, déserts, plages), atteindre 100000 Lux. De même, un film aura une sensibilité de 200 ISO. Mais que se passe-t-il entre le rayonnement solaire et le 1/500e à f:8 qu'affichent posemètres ou appareil photographiques ?
L'activité
solaire éjecte violemment et en permanence des photons vers toutes les
directions... Certains se dirigent vers une planète bleue et blanche,
la Terre ! Leur voyage sera de courte durée et un peu plus de huit minutes
plus tard (1) ils viennent heurter fortement un paysage où environ 80%
d'entre-eux seront absorbés, provoquant une partie (2) de l'échauffement
des surfaces touchées... Ce paysage se trouve éclairé par
50000 Lux dont en moyenne 18 % d'entre-eux rebondissent, créant ainsi
une luminance rendant ce paysage visible par toutes les créatures équipées
de senseurs (les yeux) capables de détecter de l'énergie dans
la bande de fréquence des 400-700 nanomètres.
Ce chiffre de 18 % correspond à un paysage reflétant la même
énergie qu'une carte "gris moyen". Les posemètres et
appareils de photo sont réglés et étalonnés pour
des sujets gris moyen, afin de centrer la majorité des sujets dans la
plage de dynamique des senseurs, qu'il soit argentiques ou numériques.
Evaluation de la luminance ou énergie réfléchie. La formule est de la forme :
Luminance = Eclairement sujet (Lux) x R (coefficient de réflexion) / Pi
La luminance s'exprime en cd/m², candelas par mètres carrés.
Cette luminance, après transformation dans le système photographique, va provoquer l'éclairement du senseur, film ou capteur numérique. Cet éclairement est dosable par un diaphragme. L'ultime étape étant constituée par l'activation dudit senseur pendant une durée déterminant son exposition. Cette durée sera bien entendu fonction des caractéristiques intrinsèques du senseur, dont sa sensibilité ISO (dépendant elle-même du traitement chimique ou logiciel associé). Le couple vitesse-diaphragme détermine la lumination
A partir de l'éclairement du sujet, de son coefficient de réflexion
et de la sensibilité du senseur, déterminons les paramètres
de l'exposition. Rappelons que les paramètres d'exposition, vitesse-diaphragme
sont résumés par les IL (Indice de lumination) ou en anglais,
EV, (pour Exposure value). Pour un éclairement donné, les IL/EV
dépendent bien entendu de la sensibilité ISO du senseur. Deux
formules permettent de considérer les cas de la lumière incidente
et de la lumière réfléchie.
Formules des posemètres
Lumière incidente : IL = (log Lux + log ISO - k) /0,3 avec k = 2,44
Lumière réfléchie : IL = (log(Lux x R / Pi) + log ISO - k) / 0,3 avec k = 1,2
Données : Eclairement 88000 Lux, 50 ISO, R = 0,18 (sujet gris moyen).
Application : ...........IL = (log(88000 x 0,18 / 3,14) + log 50 - 1,2) / 0,3 = 14
Dans ces mêmes conditions, un posemètre réglé sur 50 ISO donnerait une indication de 1/250e à f:8, soit IL = 14
Comment les posemètres convertissent les IL en couples diaphragme-vitesse ?
La vitesse V est
convertie en temps d'ouverture de l'obturateur : 1/250e = 0,004 seconde. Le
diaphragme A détermine l'éclairement du capteur.
La formule des posemètres tenant compte du diaphragme et de la vitesse
est la suivante, avec un coefficient d'adaptation k. Ici k= 1,7.
IL =(log ISO + log (A²/V) - k) / 0,3
Pour un IL et une valeur ISO donnée, c'est bien le rapport A² / V qui détermine les couples de lumination diaphragme-vitesse possibles.
Exemples : 1/1000
à f:4 donne un rapport A²/V = 16 / 0,001 = 16000
identique à 1/250 à f:8, soit 64 / 0,004 = 16000
Dans les deux cas le senseur recevra la même somme énergétique et réagira de façon identique.
(1) 150 millions
de kilomètres, parcourus à 300000 kilomètre par seconde
= 500 secondes = 8 minutes
20 secondes.
(2) La majorité
de l'échauffement provient des fréquences situées en-deça
du spectre visible, dans
l'infra-rouge.
Focale idéale
On entend fréquemment parler de "focale idéale". Quelle est donc cette focale de référence idéale ?
En
la reformulant autrement on peut poser la question :
"Quelle est la focale qui, pour un format donné,
permet de conserver la même perspective et la même vision angulaire
sur un agrandissement tenu à une distance définie, que lors de
l'observation visuelle directe ? ".
Essayons d'y répondre à partir de l'optique et de lois simples. Le tout, c'est de bien savoir de quoi on parle… Nous associerons donc des exemple concrets et appliqués, afin de faciliter la compréhension.
Il faut impérativement
que l'œil, examinant l'agrandissement, voit les mêmes objets sous
le même angle que lors de l'observation directe. Pour cela, fixons les
conditions de l'observation photographique.
1° L'agrandissement sera un A4 plein format, délivré par toutes
nos imprimantes.
2° Le sujet photographié sera par exemple une maison perpendiculaire
à l'axe de visée, d'une largeur L de 20 mètres, située
à une distance D de 30 mètres.
3° Cette maison sera vue sous un angle de ? = ATN (L/D) = 34° environ.
4° Sur un agrandissement A4, en horizontal, la largeur LA4 du format est de 0,30 mètre. Il convient également de définir la distance d'observation Do (qui joue évidemment sur l'angle). Nous prendrons 0,25 mètre (qui correspond aux statistiques de la Faculté de médecine pour la distance minimale de vision proche nette, de l'espèce humaine).
5° A partir de ces chiffres nous pouvons déterminer la largeur Lp de la maison sur l'agrandissement :
Lp = Tg (L/D) x 0,25 mètre = 0,17 m, soit 17 cm de largeur sur les 30 cm du format.
6° Pour conserver la perspective, sur un format 24 x 36 mm, la maison devra faire, en largeur, une valeur Ln fonction du rapport des formats :
Ln (en 24 x 36 mm) = 170 mm x 36 mm / 300mm = 20,4 mm.
7° Il reste à calculer quelle focale idéale Fi permettra d'obtenir cette dimension à partir d'un objet de 20 m situé à 30 m.
8° La focale idéale (dans le cadre précisé) est de : Fi = 20,4 / Tg (L/D) = 30,6 mm.
C'est un résultat
mathématique, mais basé sur la physiologie de l'œil et pouvant varier d'un individe à l'autre.
| Retour menu |